Hello everyone!
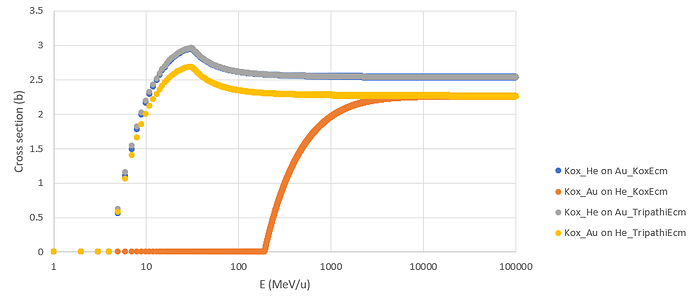
We noticed some inconsistency when plotting the cross-section values computed with the Kox and Shen models implemented in Geant4. In particular: if we take a light projectile on a heavy target system (let us say He-4 on Au-197) and compute the cross section as a function of the kinetic energy (MeV/u) of the projectile, we obtain a certain curve. When computing the cross sections for the inverse system (Au-197 on He-4) the plot looks substantially different than the direct-kinematic case.
The two plots are not supposed to be exactly the same because of the neutron excess term entering the cross-section formula, which is proportional to (A-2Z), where A and Z are the mass- and atomic- numbers of the target. (A-2Z) will in fact be equal to 39 in the direct kinematic case and equal to 0 in the inverse kinematic case, as He-4 has no neutron excess. Even if the 2 plots are not supposed to look exactly the same, they are supposed to look very similar to each other. And this is not the case. We realized the problem might have been in the computation of the center-of-mass kinetic energy. We compared the results obtained with Kox (or Shen) in both the cases of using the center-of-mass kinetic energy computation method implemented in Kox and Shen and the center-of-mass kinetic energy computation method implemented in Tripathi and Tripathi light.
Computation used in Kox and Shen:
G4double targ_mass = G4NucleiProperties::GetNuclearMass(At, Zt);
G4double proj_mass = aParticle->GetMass();
G4double proj_momentum = aParticle->GetMomentum().mag();
G4double Ecm = calEcm ( proj_mass , targ_mass , proj_momentum );
G4double G4IonsKoxCrossSection::calEcm(G4double mp, G4double mt, G4double Plab)
{
G4double Elab = std::sqrt ( mp * mp + Plab * Plab );
G4double Ecm = std::sqrt ( mp * mp + mt * mt + 2 * Elab * mt );
G4double Pcm = Plab * mt / Ecm;
G4double KEcm = std::sqrt ( Pcm * Pcm + mp * mp ) - mp;
return KEcm;
}
Computation used in Tripathi and Tripathi light:
G4double targetMass = G4ParticleTable::GetParticleTable()->GetIonTable()
->GetIonMass(G4lrint(nTargetProtons), G4lrint(targetAtomicNumber));
G4LorentzVector pTarget(0,0,0,targetMass);
G4LorentzVector pProjectile(aPart->Get4Momentum());
pTarget = pTarget+pProjectile;
G4double E_cm = (pTarget.mag()-targetMass-pProjectile.m())/MeV;
The results do not match.
We copied then the Tripathi and Tripathi light method for computing the center-of-mass kinetic energy into Kox and Shen, and as a result we obtained the type of plot we expected to obtain for Kox and Shen from previous studies.
Therefore, we would think that there is incoherence between the calculation of the Ecm values and we wanted to report it and to know your opinion about it.
Francesca and Claire-Anne