Hello everyone,
I want to create a geant4 model with a cubic volume of 20nm20nm20nm containing material B inside another volume of 100nm100nm100*nm containing material A. This structure needs to be repeated 300,000 times along X and Y. and 50,000 times along the Z axis, in total I should create 4.5 × 10¹⁵ structures.
I tried with a replica and two loops along the x and y axes, but the code crashes accidentally due to insufficient available RAM memory.
Any advise ?
Thanks and greetings.
1 Like
Doing 4.5e15 anything on a computer is hard. If you stored a single 32-bit number in every one of your voxels, you’d need 4.5e15 x 4 bytes = 18 petabytes of RAM, not to mention the data needed to define your voxel boundaries. This is well out of reach of pretty much any computer available today.
Can you reduce the discretization, or the number of repetitions?
Do you actually need such a precise structural model? Or can you make a homogenized material with the same average material properties as your model?
1 Like
I doubt very much that you can construct such a large structure on any reasonable computer. Perhaps if you explained what you are trying to simulate (i.e., the physics) someone can suggest different approaches. Could you for example use something like a large 20x20x20 structure on a first pass, and then find out which of the 8000 cells are being traversed and then, subdivide those more finley on another pass, etc?
1 Like
Thank so much you for your reply Jvavrek and Hindi.
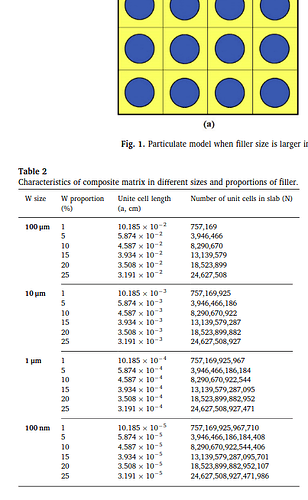
What I am trying to do is to study shielding proprieties of a polymer matrix reinforced with uniformly distributed nano-volumes filled with a tungsten.
The definition of the geometry in question has been done previously by other researchers using other general purpose Monte Carlo code as can be confirmed form the attached figure.
The range of most particles (electrons, protons, gammas) that you might want to shield against is much larger than your smallest cell size of 100 nm. Therefore the shielding property is determined mostly by the the mean composition and density, not by the particular shape of each cell. So you should be able to define a material which is a mixture of Tungsten and Polymer, with the mixing ratios detemined from your cell geometry. There may be rare cases where, for example, a particle travels mostly in the polymer but not in the Tungsten, but the solid angle for that is extremely small. What I would suggest is that you do studies in which you compare the energy deposit in a relatively small cube made of your mixed material (mean density and composition of your cell) and compare that energy deposition with the one you would get for a simulation where the geometry is made up of your cells, but a small enough number of divisions that you don’t run out of memory. So say compare the energy deposit, in a 1x1x1 mm^3 cube vs in a cube made of 100x100x100 cells each having dimensions of 10 um. I doubt you will find a difference, but you should do that first.
1 Like
Another useful trick (although I don’t know how to do this effectively in Geant4) is to impose periodic boundary conditions and only simulate a single unit cell. If a particle leaves the x+ face of your unit cell, for instance, then you re-inject it at the x- face. This way the particles “see” the entire geometry, but you don’t have to store the entire geometry all at once.
Thank you Javavrek for your suggestion.