Isomeric transition gammas from Lead neutron activation

[becepe]

Hello,
I am interested in simulating natural lead activation with 14 MeV neutrons. The specific reactions I care about are Pb207(n,n’)Pb207m and Pb208(n,2n)Pb207m. The Pb207m undergoes Isomeric Transition with 0.806 sec half-life time constant, emitting two gammas with energies 569.698 keV and 1063.656 keV.

The output I want to model is those delayed gamma, i.e., I want to correctly model the gammas’ emission time and energy. But I have not been able to get that from Geant4 yet.

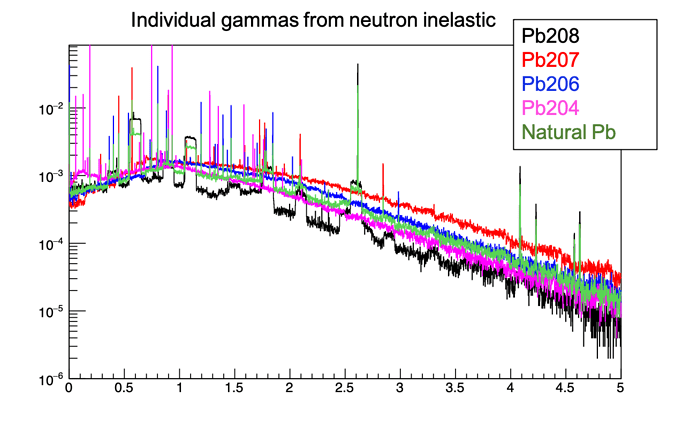
To study this, I set the lead volume to have only one isotope type at a time, and this is what I’ve found so far:

1-Gamma emission energy: individual gammas emitted from neutron inelastic processes seem to follow the decay scheme for most isotopes. I think these are mostly (n,n’) reactions.

However, for Pb208, the individually emitted gammas form “boxes” in the spectrum around the decay scheme gamma lines. See the attached plot. These would include the Pb208(n,2n) reaction gammas. When summing the total energy from all neutron inelastic processes in the event, the Pb208 spectrum boxes are “washed out” into rolling bumps.

My question: Is there a reason to expect that the inelastic gammas emitted from Pb207(n,n’)Pb207m to be modeled more accurately than those from Pb208(n,2n)Pb207m, even though they have the same final excited state.

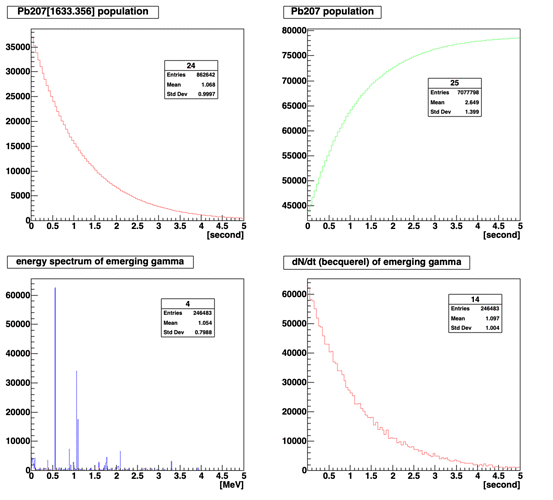
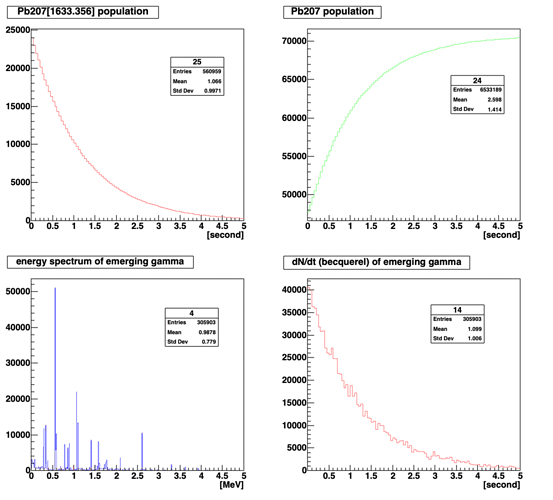
Note: It does not seem that Geant4 is actually modeling Pb207m as the final state.

2-Gamma emission time: the Pb207m isomeric transition to the ground state has a 0.806 sec half-life time constant. However, Geant4 is not producing delayed gammas with that time signature.

My question: is the isomeric transition time signature modeled in Geant4? If so, how is that turned on?

Thanks!

!

[civanch]

Hello,

what Physics List do you use? I would suggest to try out QGSP_BIC_HP.

VI

[becepe]

Hi Vladimir,
Thank you very much for your reply, and I apologize for delaying mine.
FYI, for the results above were obtained with geant4.10.05.p01 and the QGSP_BERT_HP Physics List. As you suggested, I run with QGSP_BIC_HP and got the same results.

The results do not seem to depend on any of these parameters (which I will just list below assuming you are familiar with all of them, but let me know if more detail is useful):

/process/had/particle_hp/use_photo_evaporation
/process/had/particle_hp/skip_missing_isotopes
/process/had/particle_hp/do_not_adjust_final_state
/process/had/usePreCompound
/process/deex/setIC
/process/deex/correlatedGamma
/process/deex/maxTwoJ

deex->SetStoreAllLevels
deex->SetMaxLifeTime, sec

/grdm/applyICM
/grdm/applyARM

param->SetFluo
param->SetPixe
param->SetAuger
param->SetAugerCascade
param->SetDeexcitationIgnoreCut
param->SetBeardenFluoDir

Thanks!

[maire]

NeutronHP uses PhotonEvaporation data set to modelise the deexcitation of excited states, but do not create explicitly such states.
Since Geant4 10.5, BinaryCascade generates explicitly excited ions, which can be passed to radioactiveDecay for deexcitation.
To see the difference, you can run Hadr03 with attached macro (becepe1.mac) with QGSP_BIC (or QBBC) physics constructor instead of QGSP_BIC_HP.

I have run example Activation (in extended/radioactivedecay) with macro becepe2.mac and QBBC physics constructor. On the plots, you can see that Pb207m is correctly handled.

PS: in becepe2.mac, the inactivate commands are only for simplicity; they are not essentials here.
becepe1.mac.txt (202 Bytes)
becepe2.mac.txt (628 Bytes)

[maire]

Here the macro and the plots for Pb208 activation

becepe3.mac.txt (629 Bytes)

[becepe]

Hi maire, thank you very much for taking interest in this post. I ran the example Activation, and verified the results. It is great news! Thanks!

I had selected the “HP” physics list since I also care about the rate of those neutron activations, and assumed that the “HP” list would be the appropriate one to make sure cross section data are used for neutron transport and neutron inelastic interactions (n,n’) and (n,2n). That said, it is not clear to me what 208Pb(n,2n)207mPb cross section data would Geant4 use since the only data I found in https://www.nndc.bnl.gov/exfor/endf00.jsp was EAF-2010, which I believe is not one of the datasets “HP” lists use.

I will run a test to check the rate of the 208Pb(n,2n)207mPb and 207Pb(n,n’)207mPb interactions. But I am curious as to what is your input on this.

Thanks again!

[maire]

From Hadr03 output, we can read : neutron inelastic cross section for neutron (14 MeV) on Pb207 : ~ 2.50 barn. Similar value for Pb208.
Also, similar results with G4NeutronInelasticXS data set (eg. BIC) and and G4NeutronHPInelasticXS (eg. HP).
Last year, Vladimir Ivantchenko did substantial enhancements in G4NeutronInelasticXS.
I hope he would comment himself.
Since BinaryCascade generates explicitly excited states, we can extract the contribution of the sub-channel Pb207m : ~0.3% for Pb207, 17.7% for Pb208. This cannot be done with neutronHP.
About example Activation, I admit that the output is too detailed. I suggest to modify line 75 of TrackingAction.cc :
if ((track->GetTrackID() > 1) && (meanLife != 0.)) …

[becepe]

Hello maire and Vladimir,

It has been a while since I asked this question, but just recently is that I think I understand what is happening. When I run the example Hadr03 with:

/testhadr/det/setIsotopeMat Pb208 82 208 5.94216 g/cm3 
# and
/gun/particle neutron
/gun/energy 14 MeV

the output for 1e6 primary particles, geant4.10.05.p01, and physics list BIC is:

Process calls frequency:
nCapture= 444 neutronInelastic= 999556

MeanFreePath: 22.138 cm ± 22.099 cm massic: 131.55 g/cm2
CrossSection: 0.045171 cm^-1 massic: 760.17 um2/mg
crossSection per atom: 2.6253 barn

Verification: crossSections from G4HadronicProcessStore:
nCapture= 0.34383 um2/mg 1.1874 mbarn
neutronInelastic= 760.53 um2/mg 2.6265 barn
total= 760.87 um2/mg 2.6277 barn

That total cross section matches the ENDF/B-VIII.0 cross section for PB-208(N,NON) which is about 2.62718 barn. But the contribution to the total non-elastic cross section from the reaction
208Pb(n,2n)207Pb-L1 that excites the metastable state L1, and which shows as the following in the screen output

neutron + Pb208 --> N gamma or e- + 2 neutron + Pb207[1633.356]  Q = -9.0012 MeV

is just 179746 counts. (This is the reaction that produces the delayed decay gammas 569.7 keV and 1,063.7 keV with the correct half-life of 0.806 s.)

These counts (179746 out of total =999556) correspond to about 0.47 barns. However, the cross section for that reaction is actually about 1.32 barns according to the Nuclear Energy Agency (France) Janis Web database. I think the problem is that, as ENDF/B-VIII.0 does not have data for the reaction 208Pb(n,2n)207Pb-L1, then Geant4 does not have a value for that cross section either. Does that make sense?

[becepe]

Hi maire, I added a comment to this issue and wanted to directly notify you in case you missed it. Maybe you or Vladimir have input to my comment. Thanks!

[maire]

@civanch @emendoza @ribon @becepe

I saw your mail. I need some time to remember this question …
Anyway, I put responsibles in the loop.

     Michel

[emendoza]

Dear becepe,

I don’t know about BIC, but if you are using ParticleHP (i.e. QGSP_BERT_HP or QGSP_BIC_HP) you cannot expect to see the gammas you want. The reason is because the data libraries ParticleHP uses don’t have information concerning the population of isomeric states in (n,2n) reactions. On top of this, I am not sure if the (n,n’) reactions can emit delayed gamma rays with ParticleHP. I don’t think so.

In any case, probably the best approach to solve your problem is to do the calculations in two steps. First, you compute the neutron flux in your volume, as a function of the neutron energy. Second, you multiply the obtained neutron flux by the corresponding activation cross section to get the amount of Pb-207m. This is the standard procedure to make activation calculations. You can then emit the gamma-rays coming from the decay.

Regards,

Emilio

[maire]

I repeated your exercice and, of course, found the same conclusion as you : with BIC, cross section of this channel is ~ 0.45 barn. From where comes this value ? a question for @civanch or @gunter or Dennis.
Also, I am badly surprised by the number of dummy excited states created around Pb207m.
Another question for the same people. (macro and printout attached)

Pb208.mac.txt (261 Bytes)
Pb208.out.txt (5.2 KB)

[becepe]

Dear Emilio,
Thank you for your reply on this matter few months ago. I followed your suggestions and separated my calculations in these three steps:
1- simulate the transport the neutrons thought the lead and record each step length and pre-point energy. This is the equivalent to obtaining the neutron flux through the lead.
2- “Multiply” the neutron flux by the cross section of the isomeric state Pb207m (which gets contributions from Pb2017(n,n’) and Pb208(n,2n) in natural lead) to compute the amount of Pb207m.
3- simulate the Pb207m isotope decay distributed throughout the lead.

I tested two methods “a” and “b” for step 2 to compute the amount N of Pb207m, which are explained in the attached slide. I believe method “a” is what you recommended in your post. The problem is that the results I get with method “a” do not seem to be right. The results in the second slide show that the two methods match for a large Pb volume, but they differ for a small Pb volume. Also, the “back-of-the-envelop” calculation for a thin volume matches the method “b”.

I am not sure what I may be doing wrong. So, I wanted to ask if you could explain in more detail the procedure that you had in mind for the step 2. Also, feel free to comment on the procedures described in my slides.

Thanks!

20211208_XSfoldingResults.pdf (130.5 KB)

[emendoza]

Dear becepe,

I would say that probably what you are doing wrong in method “a” is to not consider the steps where the process is “transporation”. You should consider all the processes, otherwise you are not calculating properly the neutron flux. This also explains that you have similar results with a large Pb disk and not with a small one → “transportation” process (i.e. no interaction) is “more dominant” in the small Pb volume.

Best regards,

Emilio

[becepe]

Hello Emilio, thanks again for your interest in this post. You are right that including the “transportation” steps in the method “a” calculation produces the same answer as method “b”. I checked that last week but had not updated the post yet. I guess including all steps in the method “a” is equivalent to multiplying by the incoming particle flux in the thin slab approximation (what I called "“back-of-the-envelop” calculation).
Thanks again!