X-ray photon polarization and Stokes vector

Physics Processes, Models and Cross Sections
1

I am interested in X-ray polarization.

I am doing simulation of a photon beam scattering in a plastic target. Plastic target is centered in the coordinates origin (0,0,0). The beam has continuous energy spectrum 30-75 keV. The beam is slightly divergent and it flies along direction (0,0,-1). The primary photons are unpolarized with Stokes vector (0,0,0). I am using G4EmLivermorePolarizedPhysics physics list.

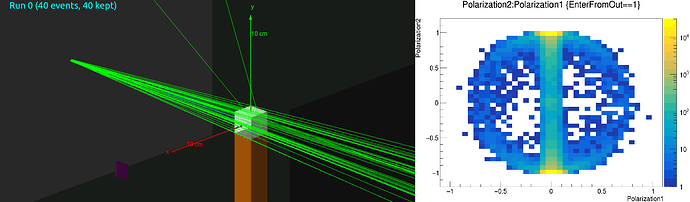
The photons get polarized by scattering in the target and the maximum polarization should be at scattering angle around 90°. Therefore I placed a silicon sensor to detect those maximally polarized photons at position (16*cm,0,0). I save Stokes vector components of every photon entering the sensor.

I am really puzzled by the results. I read the Physics Reference Manual about Stokes vector implementation in Geant4. I expected that majority of the photons would have Stokes vector close to (-1,0,0). However, simulation results show that majority of arriving photons have polarization close to (0,1,0) or (0,-1,0). That means that the photons are linearly polarized in two perpendicular planes.

The following picture shows the setup with the silicon sensor (purple) and also a 2D histogram of 2nd Stokes vector component vs. 1st Stokes vector component.

240611_Geant4_Setup_Simulation_2
240611_Geant4_Setup_Simulation_21730×507 118 KB

I don’t know whether the problem is in my simulation, in my understanding of Stokes vector and my expectations or in the physics list that I used. Could you please help me?

Is there some way in Geant4 how I could transform Stokes vector into polarization plane in global coordinates frame? I think that might help me to decipher the data.

Geant4 Version: 11.2.0
Operating System: Ubuntu 22.04
Compiler/Version: g++ 11.4.0
CMake Version: 3.22.1

1 Like
2

I returned to this problem and likely found a solution. Despite Geant4 Physics Reference Manual saying that polarization state of photons is described by Stokes vector, it is not consistent with the output of my simulation. Instead, I found that the polarization vector is always perpendicular to the momentum vector of the photon, their scalar product is zero. Therefore the polarization vector represents the direction of electric field vector in 3D space. If I use this interpretation, the results of my simulation finally make sense and they are according to my expectations.

1 Like